Quick Sort

1. Determine the running time of QuickSort for
   
   a.Sorted input
   b.reverse -ordered input
   c.random input
   d. When all the elements are equal
   
   link to solution
   
   
2. The ones who are familiar with QuickSort as also well aware of the important phase of the algorithm-the pivot selection.Suppose we always choose the middle element as the pivot .Does this make it unlikely that QuickSort will require quadratic time?
   
   link to solution
   
   
3. What is the worst-case behavior (number of comparisons) for quick sort?
   link to solution
   
4. In selecting the pivot for QuickSort, which is the best choice for optimal partitioning:
   a.The first element of the array
   b.The last element of the array
   c.The middle element of the array
   d.The largest element of the array
   e.The median of the array
   f.Any of the above
   link to solution
   
5. In its worst case QuickSort behaves like:
   a.Bubble sort
   b.Selection sort
   c.Insertion sort
   d.Bin sort
   link to solution
   
6. Describe an efficient algorithm based on Quicksort that will find the element of a set that would be at position k if the elements were sorted.
   link to solution
   
7. Recall that the linked-list version of quicksort() puts all items whose keys are equal to the pivot's key into a third queue, which doesn't need to be sorted. This can save much time if there are many repeated keys.
   
   The array-based version of quicksort() does not treat items with equal keys specially, so those items are sorted in the recursive calls.
   
   Is it possible to modify array-based quicksort() so that the array is partitioned into three parts (keys less than pivot, keys equal to pivot, keys greater than pivot) while still being in-place? (The only memory you may use is the array plus a constant amount of additional memory.)
   
   Why or why not?

Link List

Introduction

Linked list is one of the fundamental data structures, and can be used to implement other data structures. In a linked list there are different numbers of nodes. Each node is consists of two fields. The first field holds the value or data and the second field holds the reference to the next node or null if the linked list is empty.

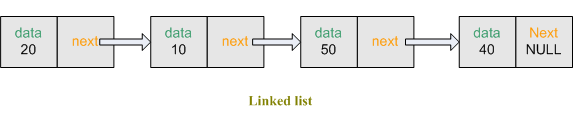
Figure: Linked list

Pseudocode:

Collapse

Linkedlist Node {
    data // The value or data stored in the node
    next // A reference to the next node, null for last node
 }

The singly-linked list is the easiest of the linked list, which has one link per node.

Pointer

To create linked list in C/C++ we must have a clear understanding about pointer. Now I will explain in brief what is pointer and how it works.

A pointer is a variable that contains the address of a variable. The question is why we need pointer? Or why it is so powerful? The answer is they have been part of the C/C++ language and so we have to use it. Using pointer we can pass argument to the functions. Generally we pass them by value as a copy. So we cannot change them. But if we pass argument using pointer, we can modify them. To understand about pointers, we must know how computer store variable and its value. Now, I will show it here in a very simple way.

Let us imagine that a computer memory is a long array and every array location has a distinct memory location.

Collapse

int a = 50 // initialize variable a 

Figure: Variable value store inside an array

It is like a house which has an address and this house has only one room. So the full address is-

Name of the house: a

Name of the person/value who live here is: 50

House Number: 4010

If we want to change the person/value of this house, the conventional way is, type this code line

Collapse

a = 100    // new initialization 

But using pointer we can directly go to the memory location of 'a' and change the person/value of this house without disturbing ‘a’. This is the main point about pointer.

Now the question is how we can use pointer. Type this code line:

Collapse

int *b;    // declare pointer b

We transfer the memory location of a to b.

Collapse

b = &a;    // the unary operator & gives the address of an object

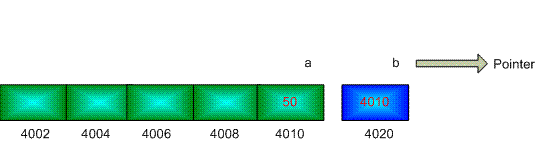
Figure: Integer pointer b store the address of the integer variable a

Now, we can change the value of a without accessing a.

Collapse

*b = 100;  // change the value of 'a' using pointer ‘b’
  cout<<a;  // show the output of 'a'

When you order the computer to access to access *b, it reads the content inside b, which is actually the address of a then it will follow the address and comes to the house of a and read a`s content which is 50.

Now the question is, if it is possible to read and change the content of b without accessing b? The answer is affirmative. We can create a pointer of pointer.

Collapse

int **c;   //declare a pointer to a pointer
 c = &b;    //transfer the address of ‘b’ to ‘c’

So, we can change the value of a without disturbing variable a and pointer b.

Collapse

**c = 200;  // change the value of ‘a’ using pointer to a pointer ‘c’
  cout<<a;  // show the output of a

Now the total code is:

Collapse

#include<iostream>
using namespace std;
 
int main()
{
      int a = 50;       // initialize integer variable a
      cout<<"The value of 'a': "<<a<<endl; // show the output of a
 
      int * b;          // declare an integer pointer b
      b = &a;           // transfer the address of 'a' to pointer 'b'
      *b = 100;         // change the value of 'a' using pointer 'b'
      cout<<"The value of 'a' using *b: "<<a<<endl;// show the output of a
 
      int **c;          // declare an integer pointer to pointer 'c'
      c = &b;           // transfer the address of 'b' to pointer to pointer 'c'
      **c = 200;        // change the value of 'a' using pointer to pointer 'c'
      cout<<"The value of 'a' using **c: "<<a<<endl;// show the output of a
 
      return 0;
}

Output:

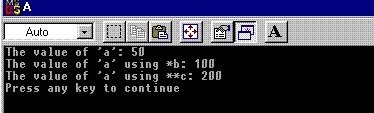
This program will give you the inside view of the pointer.

Collapse

#include<iostream>
using namespace std;
 
int main()
{
      int a = 50;       // initialize integer variable a
      cout<<"Value of 'a' = "<<a<<endl;          // show the output of a
      cout<<"Memory address of 'a': "<<&a<<endl; // show the address of a
      cout<<endl;
 
      int * b;             // declare an integer pointer b
      b = &a;              // transfer the address of 'a' to pointer 'b'
      cout<<"Value of Pointer 'b': "<<*b<<endl;  // show the output of *b
      cout<<"Content of Pointer 'b': "<<b<<endl; // show the content of *b
      cout<<"Memory address of Pointer 'b': "<<&b<<endl; // show the address of *b
      cout<<endl;
 
      int **c;                // declare an integer pointer to a pointer
      c = &b;                 // transfer the address of 'b' to 'c'
      cout<<"Value of Pointer 'c': "<<**c<<endl; // show the output of **c
      cout<<"Content of Pointer 'c': "<<c<<endl;  // show the content of **c
      cout<<"Memory address of Pointer 'c': "<<&c<<endl; // show the address of **c
      cout<<endl;
      return 0;
}

Output:

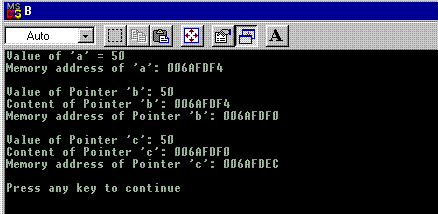
We can observe that the memory address of a and the content of pointer b is same. The content of pointer c and the memory address of b is same.

Linked list operation

Now we have a clear view about pointer. So we are ready for creating linked list.

Linked list structure

Collapse

typedef struct node                                                
{                                                               
      int data;               // will store information
      node *next;             // the reference to the next node
};                                                               

First we create a structure “node”. It has two members and first is int data which will store the information and second is node *next which will hold the address of the next node. Linked list structure is complete so now we will create linked list. We can insert data in the linked list from 'front' and at the same time from 'back’. Now we will examine how we can insert data from front in the linked list.

1) Insert from front

At first initialize node type.

Collapse

node *head = NULL;             //empty linked list

Then we take the data input from the user and store in the node info variable. Create a temporary node node *temp and allocate space for it.

Collapse

node *temp;             //create a temporary node 
temp = (node*)malloc(sizeof(node)); //allocate space for node 

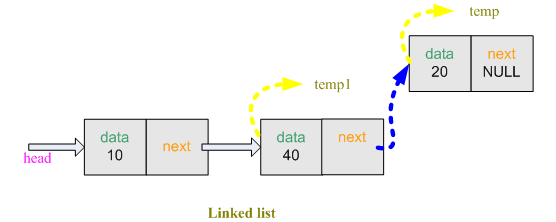
Then place info to temp->data. So the first field of the node *temp is filled. Now temp->next must become a part of the remaining linked list (although now linked list is empty but imagine that we have a 2 node linked list and head is pointed at the front) So temp->next must copy the address of the *head (Because we want insert at first) and we also want that *head will always point at front. So *head must copy the address of the node *temp.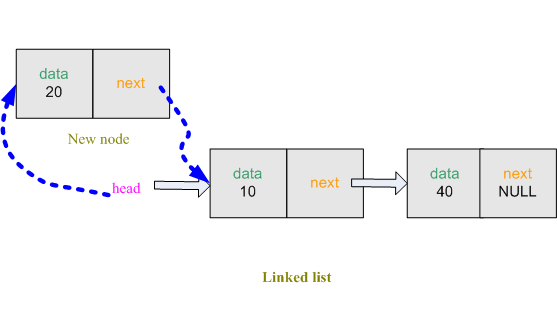

Figure: Insert at first

Collapse

temp->data = info;             // store data(first field)
temp->next=head;  // store the address of the pointer head(second field)
head = temp;                  // transfer the address of 'temp' to 'head'

2) Traverse

Now we want to see the information stored inside the linked list. We create node *temp1. Transfer the address of *head to *temp1. So *temp1 is also pointed at the front of the linked list. Linked list has 3 nodes.

We can get the data from first node using temp1->data. To get data from second node, we shift *temp1 to the second node. Now we can get the data from second node.

Collapse

while( temp1!=NULL )
{
 cout<< temp1->data<<" ";// show the data in the linked list
 temp1 = temp1->next;   // tranfer the address of 'temp->next' to 'temp'
}

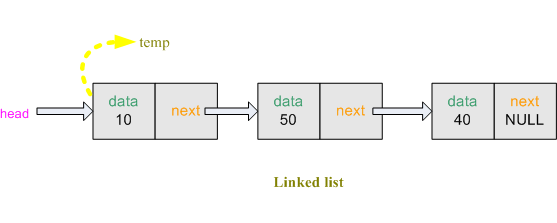
Figure: Traverse

This process will run until the linked list’s next is NULL.

3) Insert from back

Insert data from back is very similar to the insert from front in the linked list. Here the extra job is to find the last node of the linked list.

Collapse

node *temp1;                         // create a temporary node
temp1=(node*)malloc(sizeof(node));   // allocate space for node
temp1 = head;                  // transfer the address of 'head' to 'temp1'
while(temp1->next!=NULL) // go to the last node
      temp1 = temp1->next;//tranfer the address of 'temp1->next' to 'temp1'

Now, Create a temporary node node *temp and allocate space for it. Then place info to temp->data, so the first field of the node node *temp is filled. node *temp will be the last node of the linked list. For this reason, temp->next will be NULL. To create a connection between linked list and the new node, the last node of the existing linked list node *temp1`s second field temp1->next is pointed to node *temp.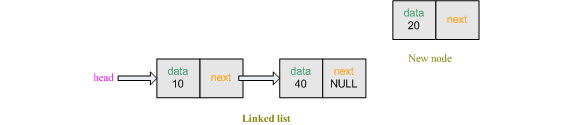

Figure: Insert at last

Collapse

node *temp;                           // create a temporary node
temp = (node*)malloc(sizeof(node));  // allocate space for node
temp->data = info;                   // store data(first field)
temp->next = NULL;                   // second field will be null(last node)
temp1->next = temp;                  // 'temp' node will be the last node

4) Insert after specified number of nodes

Insert data in the linked list after specified number of node is a little bit complicated. But the idea is simple. Suppose, we want to add a node after 2nd position. So, the new node must be in 3rd position. The first step is to go the specified number of node. Let, node *temp1 is pointed to the 2nd node now.

Collapse

cout<<"ENTER THE NODE NUMBER:";
cin>>node_number;                   // take the node number from user 
 
node *temp1;                        // create a temporary node
temp1 = (node*)malloc(sizeof(node)); // allocate space for node
temp1 = head;
 
for( int i = 1 ; i < node_number ; i++ )
{
      temp1 = temp1->next;           // go to the next node
 
      if( temp1 == NULL )
      {
            cout<<node_number<<" node is not exist"<< endl;
            break;
      }
}

Now, Create a temporary node node *temp and allocate space for it. Then place info to temp->next , so the first field of the node node *temp is filled.

Collapse

node *temp;                          // create a temporary node
temp = (node*)malloc(sizeof(node));  // allocate space for node
temp->data = info;                   // store data(first field)

To establish the connection between new node and the existing linked list, new node’s next must pointed to the 2nd node’s (temp1) next . The 2nd node’s (temp1) next must pointed to the new node(temp).

Collapse

temp->next = temp1->next;            //transfer the address of temp1->next to temp->next
temp1->next = temp;     //transfer the address of temp to temp1->next
                  

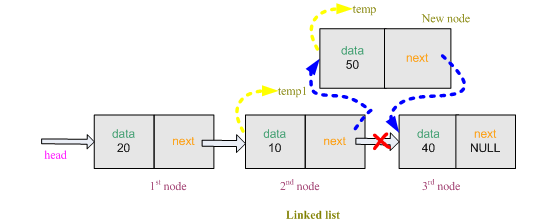
Figure: Insert after specified number of nodes

5) Delete from front

Delete a node from linked list is relatively easy. First, we create node *temp. Transfer the address of *head to *temp. So *temp is pointed at the front of the linked list. We want to delete the first node. So transfer the address of temp->next to head so that it now pointed to the second node. Now free the space allocated for first node.

Collapse

node *temp;                                      // create a temporary node
temp = (node*)malloc(sizeof(node));  // allocate space for node
temp = head;                   // transfer the address of 'head' to 'temp'
head = temp->next;      // transfer the address of 'temp->next' to 'head'
free(temp);

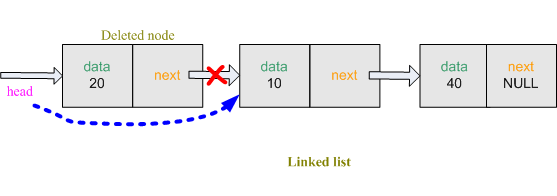
Figure: Delete at first node

6) Delete from back

The last node`s next of the linked list always pointed to NULL. So when we will delete the last node, the previous node of last nodeis now pointed at NULL. So, we will track last node and previous node of the last node in the linked list. Create temporary node * temp1 and *old_temp.

Collapse

// create a temporary node
node *temp1;
temp1 = (node*)malloc(sizeof(node)); // allocate space for node
temp1 = head;                        //transfer the address of head to temp1
node *old_temp;                     // create a temporary node
old_temp = (node*)malloc(sizeof(node));    // allocate space for node
 
while(temp1->next!=NULL)             // go to the last node
{
      old_temp = temp1; // transfer the address of 'temp1' to 'old_temp'
      temp1 = temp1->next;       // transfer the address of 'temp1->next' to 'temp1'
}

Now node *temp1 is now pointed at the last node and *old_temp is pointed at the previous node of the last node. Now rest of the work is very simple. Previous node of the last node old_temp will be NULL so it become the last node of the linked list. Free the space allocated for last lode.

Collapse

old_temp->next = NULL;         // previous node of the last node is null
free(temp1);

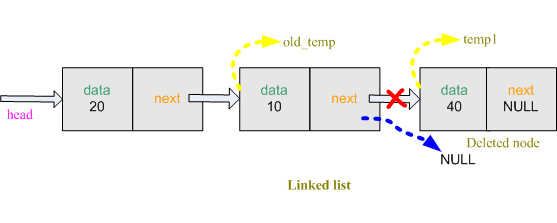
Figure: Delete at first last

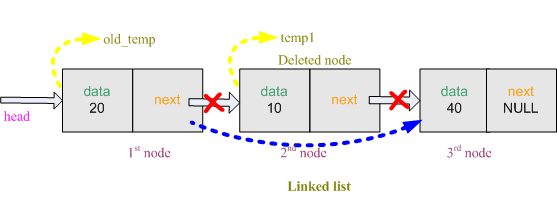
7) Delete specified number of node

To delete a specified node in the linked list, we also require to find the specified node and previous node of the specified node. Create temporary node * temp1, *old_temp and allocate space for it. Take the input from user to know the number of the node.

Collapse

node *temp1;                         // create a temporary node
temp1 = (node*)malloc(sizeof(node)); // allocate space for node
temp1 = head;                  // transfer the address of 'head' to 'temp1'
 
node *old_temp;                     // create a temporary node
old_temp = (node*)malloc(sizeof(node));    // allocate space for node
old_temp = temp1;       // transfer the address of 'temp1' to 'old_temp'

Collapse

cout<<"ENTER THE NODE NUMBER:";
cin>>node_number;                    // take location

Collapse

for( int i = 1 ; i < node_number ; i++ )
{
      old_temp = temp1;                    // store previous node
      temp1 = temp1->next;                 // store current node
 
}

Now node *temp1 is now pointed at the specified node and *old_temp is pointed at the previous node of the specified node. The previous node of the specified node must connect to the rest of the linked list so we transfer the address of temp1->next to old_temp->next. Now free the space allocated for the specified node.

Collapse

old_temp->next = temp1->next;  // transfer the address of 'temp1->next' to 'old_temp->next'
free(temp1);

8) Sort nodes

Linked list sorting is very simple. It is just like ordinary array sorting. First we create two temporary node node *temp1, *temp2 and allocate space for it. Transfer the address of first node to temp1 and address of second node to temp2. Now check if temp1->data is greater than temp2->data. If yes then exchange the data. Similarly, we perform this checking for all the nodes.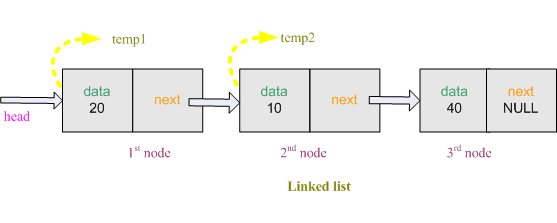

Collapse

node *temp1;                         // create a temporary node
temp1 = (node*)malloc(sizeof(node)); // allocate space for node
 
node *temp2;                         // create a temporary node
temp2 = (node*)malloc(sizeof(node)); // allocate space for node
 
int temp = 0;                        // store temporary data value
 
for( temp1 = head ; temp1!=NULL ; temp1 = temp1->next )
{
      for( temp2 = temp1->next ; temp2!=NULL ; temp2 = temp2->next )
      {
            if( temp1->data > temp2->data )
            {
                  temp = temp1->data;
                  temp1->data = temp2->data;
                  temp2->data = temp;
            }
      }
}

Conclusion

From the above discussions, I hope that everybody understands what linked list is and how we can create it. Now we can easily modify linked list according to our program requirement and try to use it for some real tasks. Those who still have some confusion about linked list, for them I will now tell you a story.

Once upon a time, an old man lived in a small village. The old man was very wise and knew many solutions about different problems. He had also special powers so he could talk to genie and spirits, and sometimes they granted his wish by using their special powers. Oneday a witch with a broom came to talk with him and ask difficult and complex issues about global warming. He was very surprised but patiently explained her about green house model and gave her advice about using biofuel in her broom. The witch was very rude and greedy but she always liked to preach her nobility. So at the time of her departure, she wanted to grant only two wishes. The old man asked her why she only granted two wishes. He also reminded her that whenever genie comes he granted two wishes.” What I am look like" the witch asked angrily,” A blank check?" The old man brewed a plan. He told her that his first wish was to get a super computer.” It is granted", the witch announced loudly.” Then my second wish is to have another two wishes”, the old man said very slowly. The witch was shell shocked. "It is also granted”, the witch said and left the place very quickly with her broom.

You may ask yourself why the witch was surprised. First, the witch granted two witches. One was fulfilled and for the second wish, the old man wanted another two wish. “What’s the big idea?” you can ask me,” The witch can also fulfill this wish”. Certainly, the witch can grant his wish. But what will happen if the old man wants to extend his second wish to another two wish set. So, the process will never end unless, the old man want to stop. The idea is same for linked list. First you have a node where you can imagine that data is the first wish and node*next is the second wish by which you can create second node just like first. This process will continue until you put NULL in the *next.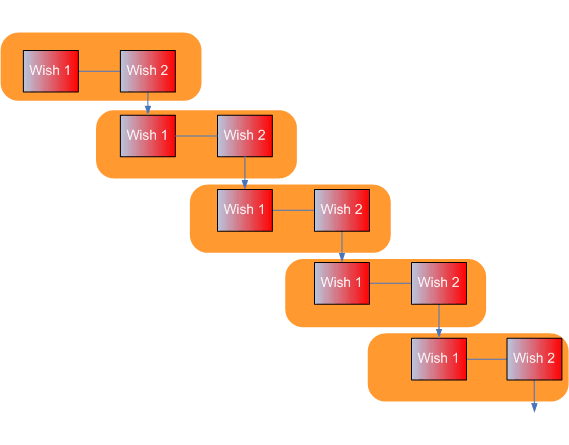

Figure: It looks like the old man had lots of wish.

References

1. Wikipedia, the free encyclopedia.
2. Pointer in C, from P. Kanetkar.

License

This article, along with any associated source code and files, is licensed under The Code Project Open License (CPOL)

About the Author

Nasif M.


Member

Bitwise operator(some nice program

Program to print Odd nos.:
#include
#include
using namespace std;
int main()
{
for(unsigned int i= 1; i <= 100; i++ )
    if( i & 0x00000001 )
        cout << i<<" ";
      getch();
}

Avoiding certain things in C/CPP

• Things to Avoid in C/C++ -- gets() , Part 1
• Things to Avoid in C/C++ -- fflush(stdin), Part 2
• Things to Avoid in C/C++ -- feof(), Part 3
• Things to Avoid in C/C++--system("pause"),Part4
  
• Things to Avoid in C/C++ -- scanf, Part 5
• Things to Avoid in C/C++ -- scanf / character, Part 6
• Things to Avoid in C/C++ -- system("pause"), Part 4
• Things to Avoid in C/C++ -- scanf / string, Part 7
• Things to Avoid in C/C++ -- scanf / number, Part 8
• Things to Avoid in C/C++ -- void main(), Part 10

Avoiding getch() funtion in dev-cpp

To avoid getch() function in dev-cpp we can use this following
function---system()
Usage:
system("PAUSE");
 Well see the post "Avoiding Certain Things in C/CPP"

Or you can add following line to the end of the program.

 return EXIT_SUCCESS;

Initialising arrays

Conside the 2D arrays: 

int anArray1[2][3] = {7};

int anArray2[3][5] =
{
{ 1, 2, 3, 4, 5, }, // row 0
{ 6, 7, 8, 9, 10, }, // row 1
{ 11, 12, 13, 14, 15 } // row 2
};

int anArray3[][5] =
{
{ 1, 2, 3, 4, 5, },
{ 6, 7, 8, 9, 10, },
{ 11, 12, 13, 14, 15 }
};

This won't work

int anArray[][] =

{

{ 1, 2, 3, 4 },

{ 5, 6, 7, 8 }

};

Initialising pointer to Arrays

   /* month_name:  return name of n-th month */
   char *month_name(int n)
   {
       static char *name[] = {
           "Illegal month",
           "January", "February", "March",
           "April", "May", "June",
           "July", "August", "September",
           "October", "November", "December"
       };

       return (n < 1 || n > 12) ? name[0] : name[n];
   }

Dynamic memory allocation

We will talk of calloc, malloc, free and realloc.
To use the four functions discussed in this section, you must include the stdlib.h header file.

Malloc and Free

#include 
#include  /* required for the malloc and free functions */

int main() {
  int number;
  int *ptr;
  int i;

  printf("How many ints would you like store? ");
  scanf("%d", &number);

  ptr = malloc(number*sizeof(int)); /* allocate memory */
 
  if(ptr!=NULL) {
    for(i=0 ; i
      *(ptr+i) = i;
    }

    for(i=number ; i>0 ; i--) {
      printf("%d\n", *(ptr+(i-1))); /* print out in reverse order */
    }

    free(ptr); /* free allocated memory */
    return 0;
  }
  else {
    printf("\nMemory allocation failed - not enough memory.\n");
    return 1;
  }
}

Calloc

Calloc is similar to malloc, but the main difference is that the values stored in the allocated memory space is zero by default. With malloc, the allocated memory could have any value.
calloc requires two arguments. The first is the number of variables you'd like to allocate memory for. The second is the size of each variable.
Like malloc, calloc will return a void pointer if the memory allocation was successful, else it'll return a NULL pointer.
This example shows you how to call calloc and also how to reference the allocated memory using an array index. The initial value of the allocated memory is printed out in the for loop.

int main()
{

float *calloc1, *calloc2, *malloc1, *malloc2;
int i;

calloc1 = calloc(3, sizeof(float)); /* might need to cast */
calloc2 = calloc(3, sizeof(float));
malloc1 = malloc(3 * sizeof(float));
malloc2 = malloc(3 * sizeof(float));

if(calloc1!=NULL && calloc2!=NULL && malloc1!=NULL && malloc2!=NULL)
{
for(i=0 ; i<3 ; i++)
{
printf("calloc1[%d] holds %05.5f, ", i, calloc1[i]);
printf("malloc1[%d] holds %05.5f\n", i, malloc1[i]);
printf("calloc2[%d] holds %05.5f, ", i, *(calloc2+i));
printf("malloc2[%d] holds %05.5f\n", i, *(malloc2+i)); }

free(calloc1); free(calloc2); free(malloc1); free(malloc2);

return 0;
}
else
{ printf("Not enough memory\n"); return 1; }
}
Output:

calloc1[0] holds 0.00000, malloc1[0] holds -431602080.00000 calloc2[0] holds 0.00000, malloc2[0] holds -431602080.00000 calloc1[1] holds 0.00000, malloc1[1] holds -431602080.00000 calloc2[1] holds 0.00000, malloc2[1] holds -431602080.00000 calloc1[2] holds 0.00000, malloc1[2] holds -431602080.00000 calloc2[2] holds 0.00000, malloc2[2] holds -431602080.00000

realloc

Now suppose you've allocated a certain number of bytes for an array but later find that you want to add values to it. You could copy everything into a larger array, which is inefficient, or you can allocate more bytes using realloc, without losing your data.
realloc takes two arguments. The first is the pointer referencing the memory. The second is the total number of bytes you want to reallocate.
Passing zero as the second argument is the equivalent of calling free.
Once again, realloc returns a void pointer if successful, else a NULL pointer is returned.

This example uses calloc to allocate enough memory for an int array of five elements. Then realloc is called to extend the array to hold seven elements.

#include
#include 

int main() {
  int *ptr;
  int i;

  ptr = calloc(5, sizeof(int));

  if(ptr!=NULL) {
    *ptr = 1;
    *(ptr+1) = 2;
    ptr[2] = 4;
    ptr[3] = 8;
    ptr[4] = 16;
    /* ptr[5] = 32; wouldn't assign anything */

    ptr = realloc(ptr, 7*sizeof(int));

    if(ptr!=NULL) {
      printf("Now allocating more memory... \n");
      ptr[5] = 32; /* now it's legal! */
      ptr[6] = 64;

      for(i=0 ; i<7 ; i++) {
        printf("ptr[%d] holds %d\n", i, ptr[i]);
      }
      realloc(ptr,0); /* same as free(ptr); - just fancier! */
      return 0;
    }
    else {
      printf("Not enough memory - realloc failed.\n");
      return 1;
    }
  }
  else {
    printf("Not enough memory - calloc failed.\n");
    return 1;
  }
}

Output:

Now allocating more memory... ptr[0] holds 1 ptr[1] holds 2 ptr[2] holds 4 ptr[3] holds 8 ptr[4] holds 16 ptr[5] holds 32 ptr[6] holds 64

Notice the two different methods I used when initializing the array: ptr[2] = 4; is the equivalent to *(ptr+2) = 4; (just easier to read!).
Before using realloc, assigning a value to ptr[5] wouldn't cause a compile error. The program would still run, but ptr[5] wouldn't hold the value you assigned.

Passing 2 D array to function

double f(double values[][4], int n);

int main() {
  double beans[3][4] = {
                         { 1.0,  2.0,  3.0,  4.0},
                         { 5.0,  6.0,  7.0,  8.0},
                         { 9.0, 10.0, 11.0, 12.0}
                       };

 printf(" %f\n",f(beans, sizeof beans/sizeof beans[0]));
 getch();
  return 0;
}

double f(double array[][4], int size) {
  double sum = 0.0;
  int i,j;
  for( i = 0 ; i < size ; i++)      
    for( j = 0 ; j < 4 ; j++)       
      sum += array[i][j];
     
  return sum;
}

Another method is you dynamically allocate array and than pass its pointer to the function.
#include
#include
#include
// Ref : http://www.eskimo.com/~scs/cclass/int/sx9b.html
void printArray(int **array, int m, int n)
{
     int i,j;
 for(i=0;i
   for( j=0;j
printf("%d\n",array[i][j]);

     printf("\n");
}
int main()
{
      int i,j,k=0, m=5, n=20;
      int **a=(int **)malloc(m*sizeof(int *));
      for(i=0;i
      for(i=0;i      //for(i=0;i
      printArray(a,m,n);
      system("PAUSE");
      return 0;
}

Multi-dimensional arrays

#include

#include

int main() {

int a[3][3][3][3];

//it gives address of a[0][0][0][0] .

printf(" \n address of array a is %u", a);

printf("\n address of a[2][0][0][0] is %u , "

"given by a[2] , %u given by a+2",

a[2], a + 2);

printf("\n address of a[2][2][0][0] is %u , "

"given by a[2][2] , %u given by a[2]+2",

a[2][2], a[2] + 2);

printf("\n address of a[2][2][1][0] is %u , "

"given by a[2][2][1] , %u given by a[2][2]+1",

a[2][2][1], a[2][2] + 1);

return 0;

}

Output for instance:

address of array a is 65340
address of a[2][0][0][0] is 65448, given by a[2] , 65448 given by a+2
address of a[2][2][0][0] is 65484, given by a[2][2] ,65484 given by a[2]+2
address of a[2][2][1][0] is 65490, given by a[2][2][1] , 65490 given by a[2][2]+1

Expanation :

a[i][j] = a[i]+j and so on apply the rule

Congruence

Consider the integers Z := {. . . ,−2,−1, 0, 1, 2, . . .}. For a, b 2 Z, we say
that b divides a, or alternatively, that a is divisible by b, if there exists
c 2 Z such that a = bc. If b divides a, then b is called a divisor of a, and
we write b | a. If b does not divide a, then we write b - a.
We first state some simple facts:
Theorem 1.1. For all a, b, c 2 Z, we have
(i) a | a, 1 | a, and a | 0;
(ii) 0 | a if and only if a = 0;
(iii) a | b and a | c implies a | (b + c);
(iv) a | b implies a | −b;
(v) a | b and b | c implies a | c.

Zero in history

I have left mathematics since long...and have to start giving time to it again....so starting with zero...I would try to write in chronological order, but there's some overlap. Also when possible I will include the date of the earliest known usage of the symbol, and a picture of said symbol.

BABYLONIAN:

The Babylonians inherited the unholy number/cuneiform writing system originally developed by the Sumerians. This civilization ran in a fairly unbroken line for thousands of years, with breaks to change names and move locations. So while I was talking the other day about Sumerians and base sixty, THOSE Sumerians were about four thousand years back from THESE Babylonians.

That said, the 'double wedge' shown above is considered a symbol "to indicate the absence of units of a given order of magnitude" (from Georges Ifrah). Meaning it was used just like our zero today. Their notation system DID use positions like ours does, but because of the base sixty, it was not a simple progression by tens like ours is - 1, 10, 100, 1000, etc. Their system went up in sixties (near as I can figure without the degree in advanced math I'm not ever getting): 1, 60, 3600, 216000. The exact 'steps' of the system vary a bit over the four or five thousand years the civilization shifted around, but by the time they settled on a positional notation system about 2000 BCE, that was generally how they did it. Interestingly, I think, is that they used the positional notation system for about two thousand years before finally inventing (or deciding to use) a zero symbol, under the Selucid Turks in about 300 BCE.


MAYAN:

The Mayans seem to have had TWO types of zero, to go with their two types of writing. The first kind was a fairly straightforward text style that was used for actually doing mathematical computation; the zero from that system is the eye-shaped symbol in the upper left of the picture. The second type of writing was the flowery symbolic 'writing' they used for monuments, shown in the bottom row of the above picture - there were several versions of the zero used for monuments. Mostly they look like four-petaled flowers. They'd make a cool tattoo for a math history geek.

The Mayans are kind of entertaining because they only NEEDED the first zero. The Mayans ran on base twenty and wrote their numbers out much the same way we do in base ten, with the positional notation and all (ones, twenties, four hundreds, etc). It was an efficient system, which is probably why the Maya were some of the best mathematicians in the ancient world. However, when they did inscriptions on monuments, they wrote their numbers out formally, so - for instance - 1234 would be written out "one thousand, two hundreds, three tens, four ones". Obviously for that kind of system you don't need a zero to hold a place, you just skip the empty positions - 1000 would be "one thousand". But for religious and aesthetic purposes, the Mayans liked to spell it out. "One thousand, zero hundreds, zero tens, zero ones." So it's a useless sort of zero, though kinda pretty.

Their real zero, in their math papers and notes, dates back to at least 300 BCE. Our understanding of the Mayans is kind of sketchy thanks to Christian missionaries torching huge piles of their manuscripts, so it's possible the New World zero is older. We just don't know.


INDIAN/ARAB/WESTERN:

This one is ours; you can see the evolution of it above, as it traveled along the trade routes from India, where it was invented (along with the rest of the positional notation system), to the Arabs, and then to Western Civilization.

There is a text (the Ganitasarasamgraha, if you must know) dated to 850 CE that has calculations that math types agree HAD to be done with some kind of positional notation. Experts claim from analysis of complex manuscripts that the entire system - positional notation and a use of zero for empty 'slots' - was in place by about 950 CE but not much before that. There appears to be some kind of academic slug-fest over these dates, with accusations of forgery and misinterpretation flying about, so have a big grain of salt with this. (Personally, I suspect the system goes back further and we just haven't found evidence of it yet.) There is, in fact, commentary by an Arab dude (Severus Sebokt; no, I did not make that up) written in 662 CE, talking about how the Greeks didn't know jack and just inherited their civilization from the Middle East, and how the Hindus had a better number system that ran on 'only nine figures'. This is interesting for two reasons. First, of course is the implication that the base ten system is older than the Hindu manuscripts can demonstrate, and second is that even in the 600s, people were sick to death of hearing about how awesome the Greeks are (I'm in august company).

From there, the system moved over to the Arabs, who were busy dominating the trade routes between east and west and making big bucks off it. They needed a good system to count their big bucks, and adopted the Indian base-ten-with-zero method to do so. We're not sure when it happened - more academic slug-fests there - but by looking at the symbols above, anyone, even those of us with no official training, can see the evolution.

Western civ is said to have discovered the numbers while slogging about, killing people, during the crusades. I'm kinda skeptical. I think what really happened is the system oozed north from Spain (which was held by Arab peoples from 711 to 1492 CE) and west from Byzantium which, while considered European, had Asian trade routes running through it constantly, and had close ties to Western Europe until it was taken by the Ottoman Turks in 1453 CE. Just like most of the rest of Arab knowledge got into Europe (including knitting).


There you go, those are the high points anyway. I'm sure there are thousands of gory details I could have included, but I wanted a brief overview, not a dissertation.

At the moment, I feel an urge to write about the Phonecians. I'm tired of numbers.

History of Mathematics in India
In all early civilizations, the first expression of mathematical understanding appears in the form of counting systems. Numbers in very early societies were typically represented by groups of lines, though later different numbers came to be assigned specific numeral names and symbols (as in India) or were designated by alphabetic letters (such as in Rome). Although today, we take our decimal system for granted, not all ancient civilizations based their numbers on a ten-base system. In ancient Babylon, a sexagesimal (base 60) system was in use.

The Decimal System in Harappa

In India a decimal system was already in place during the Harappan period, as indicated by an analysis of Harappan weights and measures. Weights corresponding to ratios of 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, and 500 have been identified, as have scales with decimal divisions. A particularly notable characteristic of Harappan weights and measures is their remarkable accuracy. A bronze rod marked in units of 0.367 inches points to the degree of precision demanded in those times. Such scales were particularly important in ensuring proper implementation of town planning rules that required roads of fixed widths to run at right angles to each other, for drains to be constructed of precise measurements, and for homes to be constructed according to specified guidelines. The existence of a gradated system of accurately marked weights points to the development of trade and commerce in Harappan society.

Mathematical Activity in the Vedic Period

In the Vedic period, records of mathematical activity are mostly to be found in Vedic texts associated with ritual activities. However, as in many other early agricultural civilizations, the study of arithmetic and geometry was also impelled by secular considerations. Thus, to some extent early mathematical developments in India mirrored the developments in Egypt, Babylon and China . The system of land grants and agricultural tax assessments required accurate measurement of cultivated areas. As land was redistributed or consolidated, problems of mensuration came up that required solutions. In order to ensure that all cultivators had equivalent amounts of irrigated and non-irrigated lands and tracts of equivalent fertility - individual farmers in a village often had their holdings broken up in several parcels to ensure fairness. Since plots could not all be of the same shape - local administrators were required to convert rectangular plots or triangular plots to squares of equivalent sizes and so on. Tax assessments were based on fixed proportions of annual or seasonal crop incomes, but could be adjusted upwards or downwards based on a variety of factors. This meant that an understanding of geometry and arithmetic was virtually essential for revenue administrators. Mathematics was thus brought into the service of both the secular and the ritual domains.

Arithmetic operations (Ganit) such as addition, subtraction, multiplication, fractions, squares, cubes and roots are enumerated in the Narad Vishnu Purana attributed to Ved Vyas (pre-1000 BC). Examples of geometric knowledge (rekha-ganit) are to be found in the Sulva-Sutras of Baudhayana (800 BC) and Apasthmaba (600 BC) which describe techniques for the construction of ritual altars in use during the Vedic era. It is likely that these texts tapped geometric knowledge that may have been acquired much earlier, possibly in the Harappan period. Baudhayana's Sutra displays an understanding of basic geometric shapes and techniques of converting one geometric shape (such as a rectangle) to another of equivalent (or multiple, or fractional) area (such as a square). While some of the formulations are approximations, others are accurate and reveal a certain degree of practical ingenuity as well as some theoretical understanding of basic geometric principles. Modern methods of multiplication and addition probably emerged from the techniques described in the Sulva-Sutras.
Pythagoras - the Greek mathematician and philosopher who lived in the 6th C B.C was familiar with the Upanishads and learnt his basic geometry from the Sulva Sutras. An early statement of what is commonly known as the Pythagoras theorem is to be found in Baudhayana's Sutra: The chord which is stretched across the diagonal of a square produces an area of double the size. A similar observation pertaining to oblongs is also noted. His Sutra also contains geometric solutions of a linear equation in a single unknown. Examples of quadratic equations also appear. Apasthamba's sutra (an expansion of Baudhayana's with several original contributions) provides a value for the square root of 2 that is accurate to the fifth decimal place. Apasthamba also looked at the problems of squaring a circle, dividing a segment into seven equal parts, and a solution to the general linear equation. Jain texts from the 6th C BC such as the Surya Pragyapti describe ellipses.
Modern-day commentators are divided on how some of the results were generated. Some believe that these results came about through hit and trial - as rules of thumb, or as generalizations of observed examples. Others believe that once the scientific method came to be formalized in the Nyaya-Sutras - proofs for such results must have been provided, but these have either been lost or destroyed, or else were transmitted orally through the Gurukul system, and only the final results were tabulated in the texts. In any case, the study of Ganit i.e mathematics was given considerable importance in the Vedic period. The Vedang Jyotish (1000 BC) includes the statement: "Just as the feathers of a peacock and the jewel-stone of a snake are placed at the highest point of the body (at the forehead), similarly, the position of Ganit is the highest amongst all branches of the Vedas and the Shastras."
(Many centuries later, Jain mathematician from Mysore, Mahaviracharya further emphasized the importance of mathematics: "Whatever object exists in this moving and non-moving world, cannot be understood without the base of Ganit (i.e. mathematics)".)

Panini and Formal Scientific Notation

A particularly important development in the history of Indian science that was to have a profound impact on all mathematical treatises that followed was the pioneering work by Panini (6th C BC) in the field of Sanskrit grammar and linguistics. Besides expounding a comprehensive and scientific theory of phonetics, phonology and morphology, Panini provided formal production rules and definitions describing Sanskrit grammar in his treatise called Asthadhyayi. Basic elements such as vowels and consonants, parts of speech such as nouns and verbs were placed in classes. The construction of compound words and sentences was elaborated through ordered rules operating on underlying structures in a manner similar to formal language theory.

Today, Panini's constructions can also be seen as comparable to modern definitions of a mathematical function. G G Joseph, in The crest of the peacock argues that the algebraic nature of Indian mathematics arises as a consequence of the structure of the Sanskrit language. Ingerman in his paper titled Panini-Backus form finds Panini's notation to be equivalent in its power to that of Backus - inventor of the Backus Normal Form used to describe the syntax of modern computer languages. Thus Panini's work provided an example of a scientific notational model that could have propelled later mathematicians to use abstract notations in characterizing algebraic equations and presenting algebraic theorems and results in a scientific format.

Philosophy and Mathematics

Philosophical doctrines also had a profound influence on the development of mathematical concepts and formulations. Like the Upanishadic world view, space and time were considered limitless in Jain cosmology. This led to a deep interest in very large numbers and definitions of infinite numbers. Infinite numbers were created through recursive formulae, as in the Anuyoga Dwara Sutra. Jain mathematicians recognized five different types of infinities: infinite in one direction, in two directions, in area, infinite everywhere and perpetually infinite. Permutations and combinations are listed in the Bhagvati Sutras (3rd C BC) and Sathananga Sutra (2nd C BC).

Jain set theory probably arose in parallel with the Syadvada system of Jain epistemology in which reality was described in terms of pairs of truth conditions and state changes. The Anuyoga Dwara Sutra demonstrates an understanding of the law of indeces and uses it to develop the notion of logarithms. Terms like Ardh Aached , Trik Aached, and Chatur Aached are used to denote log base 2, log base 3 and log base 4 respectively. In Satkhandagama various sets are operated upon by logarithmic functions to base two, by squaring and extracting square roots, and by raising to finite or infinite powers. The operations are repeated to produce new sets. In other works the relation of the number of combinations to the coefficients occurring in the binomial expansion is noted.
Since Jain epistemology allowed for a degree of indeterminacy in describing reality, it probably helped in grappling with indeterminate equations and finding numerical approximations to irrational numbers.

Buddhist literature also demonstrates an awareness of indeterminate and infinite numbers. Buddhist mathematics was classified either as Garna (Simple Mathematics) or Sankhyan (Higher Mathematics). Numbers were deemed to be of three types: Sankheya (countable), Asankheya (uncountable) and Anant (infinite).

Philosophical formulations concerning Shunya - i.e. emptiness or the void may have facilitated in the introduction of the concept of zero. While the zero (bindu) as an empty place holder in the place-value numeral system appears much earlier, algebraic definitions of the zero and it's relationship to mathematical functions appear in the mathematical treatises of Brahmagupta in the 7th C AD. Although scholars are divided about how early the symbol for zero came to be used in numeric notation in India, (Ifrah arguing that the use of zero is already implied in Aryabhatta) tangible evidence for the use of the zero begins to proliferate towards the end of the Gupta period. Between the 7th C and the 11th C, Indian numerals developed into their modern form, and along with the symbols denoting various mathematical functions (such as plus, minus, square root etc) eventually became the foundation stones of modern mathematical notation.

The Indian Numeral System

Although the Chinese were also using a decimal based counting system, the Chinese lacked a formal notational system that had the abstraction and elegance of the Indian notational system, and it was the Indian notational system that reached the Western world through the Arabs and has now been accepted as universal. Several factors contributed to this development whose significance is perhaps best stated by French mathematician, Laplace: "The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. It's simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions."

Brilliant as it was, this invention was no accident. In the Western world, the cumbersome roman numeral system posed as a major obstacle, and in China the pictorial script posed as a hindrance. But in India, almost everything was in place to favor such a development. There was already a long and established history in the use of decimal numbers, and philosophical and cosmological constructs encouraged a creative and expansive approach to number theory. Panini's studies in linguistic theory and formal language and the powerful role of symbolism and representational abstraction in art and architecture may have also provided an impetus, as might have the rationalist doctrines and the exacting epistemology of the Nyaya Sutras, and the innovative abstractions of the Syadavada and Buddhist schools of learning.

Influence of Trade and Commerce, Importance of Astronomy

The growth of trade and commerce, particularly lending and borrowing demanded an understanding of both simple and compound interest which probably stimulated the interest in arithmetic and geometric series. Brahmagupta's description of negative numbers as debts and positive numbers as fortunes points to a link between trade and mathematical study. Knowledge of astronomy - particularly knowledge of the tides and the stars was of great import to trading communities who crossed oceans or deserts at night. This is borne out by numerous references in the Jataka tales and several other folk-tales. The young person who wished to embark on a commercial venture was inevitably required to first gain some grounding in astronomy. This led to a proliferation of teachers of astronomy, who in turn received training at universities such as at Kusumpura (Bihar) or Ujjain (Central India) or at smaller local colleges or Gurukuls. This also led to the exchange of texts on astronomy and mathematics amongst scholars and the transmission of knowledge from one part of India to another. Virtually every Indian state produced great mathematicians who wrote commentaries on the works of other mathematicians (who may have lived and worked in a different part of India many centuries earlier). Sanskrit served as the common medium of scientific communication.

The science of astronomy was also spurred by the need to have accurate calendars and a better understanding of climate and rainfall patterns for timely sowing and choice of crops. At the same time, religion and astrology also played a role in creating an interest in astronomy and a negative fallout of this irrational influence was the rejection of scientific theories that were far ahead of their time. One of the greatest scientists of the Gupta period - Aryabhatta (born in 476 AD, Kusumpura, Bihar) provided a systematic treatment of the position of the planets in space. He correctly posited the axial rotation of the earth, and inferred correctly that the orbits of the planets were ellipses. He also correctly deduced that the moon and the planets shined by reflected sunlight and provided a valid explanation for the solar and lunar eclipses rejecting the superstitions and mythical belief systems surrounding the phenomenon. Although Bhaskar I (born Saurashtra, 6th C, and follower of the Asmaka school of science, Nizamabad, Andhra ) recognized his genius and the tremendous value of his scientific contributions, some later astronomers continued to believe in a static earth and rejected his rational explanations of the eclipses. But in spite of such setbacks, Aryabhatta had a profound influence on the astronomers and mathematicians who followed him, particularly on those from the Asmaka school.

Mathematics played a vital role in Aryabhatta's revolutionary understanding of the solar system. His calculations on pi, the circumferance of the earth (62832 miles) and the length of the solar year (within about 13 minutes of the modern calculation) were remarkably close approximations. In making such calculations, Aryabhatta had to solve several mathematical problems that had not been addressed before including problems in algebra (beej-ganit) and trigonometry (trikonmiti).

Bhaskar I continued where Aryabhatta left off, and discussed in further detail topics such as the longitudes of the planets; conjunctions of the planets with each other and with bright stars; risings and settings of the planets; and the lunar crescent. Again, these studies required still more advanced mathematics and Bhaskar I expanded on the trigonometric equations provided by Aryabhatta, and like Aryabhatta correctly assessed pi to be an irrational number. Amongst his most important contributions was his formula for calculating the sine function which was 99% accurate. He also did pioneering work on indeterminate equations and considered for the first time quadrilaterals with all the four sides unequal and none of the opposite sides parallel.

Another important astronomer/mathematician was Varahamira (6th C, Ujjain) who compiled previously written texts on astronomy and made important additions to Aryabhatta's trigonometric formulas. His works on permutations and combinations complemented what had been previously achieved by Jain mathematicians and provided a method of calculation of nCr that closely resembles the much more recent Pascal's Triangle. In the 7th century, Brahmagupta did important work in enumerating the basic principles of algebra. In addition to listing the algebraic properties of zero, he also listed the algebraic properties of negative numbers. His work on solutions to quadratic indeterminate equations anticipated the work of Euler and Lagrange.

Emergence of Calculus

In the course of developing a precise mapping of the lunar eclipse, Aryabhatta was obliged to introduce the concept of infinitesimals - i.e. tatkalika gati to designate the infinitesimal, or near instantaneous motion of the moon, and express it in the form of a basic differential equation. Aryabhatta's equations were elaborated on by Manjula (10th C) and Bhaskaracharya (12th C) who derived the differential of the sine function. Later mathematicians used their intuitive understanding of integration in deriving the areas of curved surfaces and the volumes enclosed by them.

Applied Mathematics, Solutions to Practical Problems

Developments also took place in applied mathematics such as in creation of trigonometric tables and measurement units. Yativrsabha's work Tiloyapannatti (6th C) gives various units for measuring distances and time and also describes the system of infinite time measures.

In the 9th C, Mahaviracharya ( Mysore) wrote Ganit Saar Sangraha where he described the currently used method of calculating the Least Common Multiple (LCM) of given numbers. He also derived formulae to calculate the area of an ellipse and a quadrilateral inscribed within a circle (something that had also been looked at by Brahmagupta) The solution of indeterminate equations also drew considerable interest in the 9th century, and several mathematicians contributed approximations and solutions to different types of indeterminate equations.

In the late 9th C, Sridhara (probably Bengal) provided mathematical formulae for a variety of practical problems involving ratios, barter, simple interest, mixtures, purchase and sale, rates of travel, wages, and filling of cisterns. Some of these examples involved fairly complicated solutions and his Patiganita is considered an advanced mathematical work. Sections of the book were also devoted to arithmetic and geometric progressions, including progressions with fractional numbers or terms, and formulas for the sum of certain finite series are provided. Mathematical investigation continued into the 10th C. Vijayanandi (of Benares, whose Karanatilaka was translated by Al-Beruni into Arabic) and Sripati of Maharashtra are amongst the prominent mathematicians of the century.

The leading light of 12th C Indian mathematics was Bhaskaracharya who came from a long-line of mathematicians and was head of the astronomical observatory at Ujjain. He left several important mathematical texts including the Lilavati and Bijaganita and the Siddhanta Shiromani, an astronomical text. He was the first to recognize that certain types of quadratic equations could have two solutions. His Chakrawaat method of solving indeterminate solutions preceded European solutions by several centuries, and in his Siddhanta Shiromani he postulated that the earth had a gravitational force, and broached the fields of infinitesimal calculation and integration. In the second part of this treatise, there are several chapters relating to the study of the sphere and it's properties and applications to geography, planetary mean motion, eccentric epicyclical model of the planets, first visibilities of the planets, the seasons, the lunar crescent etc. He also discussed astronomical instruments and spherical trigonometry. Of particular interest are his trigonometric equations: sin(a + b) = sin a cos b + cos a sin b; sin(a - b) = sin a cos b - cos a sin b;

The Spread of Indian Mathematics

The study of mathematics appears to slow down after the onslaught of the Islamic invasions and the conversion of colleges and universities to madrasahs. But this was also the time when Indian mathematical texts were increasingly being translated into Arabic and Persian. Although Arab scholars relied on a variety of sources including Babylonian, Syriac, Greek and some Chinese texts, Indian mathematical texts played a particularly important role. Scholars such as Ibn Tariq and Al-Fazari (8th C, Baghdad), Al-Kindi (9th C, Basra), Al-Khwarizmi (9th C. Khiva), Al-Qayarawani (9th C, Maghreb, author of Kitab fi al-hisab al-hindi), Al-Uqlidisi (10th C, Damascus, author of The book of Chapters in Indian Arithmetic), Ibn-Sina (Avicenna), Ibn al-Samh (Granada, 11th C, Spain), Al-Nasawi (Khurasan, 11th C, Persia), Al-Beruni (11th C, born Khiva, died Afghanistan), Al-Razi (Teheran), and Ibn-Al-Saffar (11th C, Cordoba) were amongst the many who based their own scientific texts on translations of Indian treatises. Records of the Indian origin of many proofs, concepts and formulations were obscured in the later centuries, but the enormous contributions of Indian mathematics was generously acknowledged by several important Arabic and Persian scholars, especially in Spain. Abbasid scholar Al-Gaheth wrote: " India is the source of knowledge, thought and insight”. Al-Maoudi (956 AD) who travelled in Western India also wrote about the greatness of Indian science. Said Al-Andalusi, an 11th C Spanish scholar and court historian was amongst the most enthusiastic in his praise of Indian civilization, and specially remarked on Indian achievements in the sciences and in mathematics. Of course, eventually, Indian algebra and trigonometry reached Europe through a cycle of translations, traveling from the Arab world to Spain and Sicily, and eventually penetrating all of Europe. At the same time, Arabic and Persian translations of Greek and Egyptian scientific texts become more readily available in India.

The Kerala School

Although it appears that original work in mathematics ceased in much of Northern India after the Islamic conquests, Benaras survived as a center for mathematical study, and an important school of mathematics blossomed in Kerala. Madhava (14th C, Kochi) made important mathematical discoveries that would not be identified by European mathematicians till at least two centuries later. His series expansion of the cos and sine functions anticipated Newton by almost three centuries. Historians of mathematics, Rajagopal, Rangachari and Joseph considered his contributions instrumental in taking mathematics to the next stage, that of modern classical analysis. Nilkantha (15th C, Tirur, Kerala) extended and elaborated upon the results of Madhava while Jyesthadeva (16th C, Kerala) provided detailed proofs of the theorems and derivations of the rules contained in the works of Madhava and Nilkantha. It is also notable that Jyesthadeva's Yuktibhasa which contained commentaries on Nilkantha's Tantrasamgraha included elaborations on planetary theory later adopted by Tycho Brahe, and mathematics that anticipated work by later Europeans. Chitrabhanu (16th C, Kerala) gave integer solutions to twenty-one types of systems of two algebraic equations, using both algebraic and geometric methods in developing his results. Important discoveries by the Kerala mathematicians included the Newton-Gauss interpolation formula, the formula for the sum of an infinite series, and a series notation for pi. Charles Whish (1835, published in the Transactions of the Royal Asiatic Society of Great Britain and Ireland) was one of the first Westerners to recognize that the Kerala school had anticipated by almost 300 years many European developments in the field.

Yet, few modern compendiums on the history of mathematics have paid adequate attention to the often pioneering and revolutionary contributions of Indian mathematicians. But as this essay amply demonstrates, a significant body of mathematical works were produced in the Indian subcontinent. The science of mathematics played a pivotal role not only in the industrial revolution but in the scientific developments that have occurred since. No other branch of science is complete without mathematics. Not only did India provide the financial capital for the industrial revolution (see the essay on colonization) India also provided vital elements of the scientific foundation without which humanity could not have entered this modern age of science and high technology.